Paper presented at Symposium on Frontiers of Chemistry- in Conjunction with the Second Conference for Worldwide Chinese Young Chemists (CWCYC-2), The Hong Kong University of Science and Technology, 20-23 December 1997, Hong Kong
Indistinguishability Principle and Symmetry Principle
Shu-Kun Lin
Molecular Diversity Preservation International (MDPI), Saengergasse 25, CH-4054 Basel, Switzerland (e-mail: [email protected], http://www.mdpi.org/lin.htm)
The Gibbs paradox statement [1] which has been a very fundamental assumption in statistical mechanics says that the entropy of mixing or assembling to form solid assemblages, liquid and gas mixtures or any other analogous assemblages such as quantum states, decreases discontinuously (Fig.1a) with the increase in the property similarity of the composing individuals [1g]. Some authors revised the Gibbs paradox statement and argued that the entropy of mixing decreases continuously with the increase in the property similarity of the composing individuals (Fig.1b) [1a,1b,1d]. This statement has been discarded and a new theory constructed: entropy of mixing or assembling increases continuously (Fig.1c) with the increase in the similarity, based on the following experimental evidences and theoretical arguments [2]:
Facts: (a) Mixing of hydrocarbons in water (hydrophobic effect). Different substances do not mix but separate, as a consequence of the fact that the indistinguishable subsystems are the most spontaneously miscible ones. (b) Degenerate reactions where the reactant and the product are exactly the same, and resonance (mixing of the quantum states). (c) Information registration process (![]() ) is a process of assembling different species. (d) All the symmetry breaking phenomena which show that the assembling of indistinguishable subsystems is the most spontaneous process.
) is a process of assembling different species. (d) All the symmetry breaking phenomena which show that the assembling of indistinguishable subsystems is the most spontaneous process.
Theoretical arguments: (a) From the well-known inequality
![]() (1)
(1)
and the general entropy expression
![]() (2)
(2)
the condition for the maximum entropy must be the indistinguishability. (b) The Gibbs paradox statement of entropy of mixing contradicts with the entropy additivity principle suggested by Gibbs himself. The Gibbs entropy additivity principle should be the same in form as the Dalton pressure additivity for ideal gases. (c) An ideal gas is defined as a gas consisting of independent particles. However, the inclusion of the term ![]() in the Sackur-Tetrode entropy formula according to Gibbs implies that the N particles in consideration are not independent.
in the Sackur-Tetrode entropy formula according to Gibbs implies that the N particles in consideration are not independent.
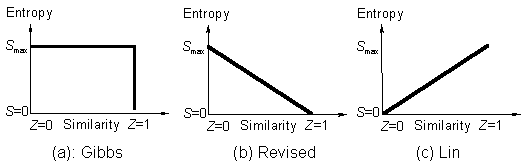
Figure 1. Correlation of the entropy of mixing with similarity.
Given two systems which are identical in material contents, energies, and all the other properties except their symmetries which are the only difference. Which system would be more stable, the one with higher symmetry or the one with lower symmetry? For a solid phase, is the crystalline structure or the non-crystalline structure more stable?
In answering this structural relative stability question, the entropy S is a pertinent thermodynamic function to consider. However, according to all statistical mechanics [1], such as the treatment of the Ising model of symmetry breaking problems, higher symmetry in a system would imply a lower value of S, and the answer would be that the less symmetrical static structure is more stable. That is incorrect. A logarithmic relation (eq 3) has been established [2] which conforms with the symmetry principle [3]. For a system of w microstates,
![]() (3)
(3)
(k is positive) and the apparent symmetry number or apparent indistinguishability number [4] is
![]() (4)
(4)
where ![]() is the probability of the ith microstate. In conclusion, a higher value of entropy of any system correlates to a higher symmetry and a higher indistinguishability of both dynamic systems and static structures [2].
is the probability of the ith microstate. In conclusion, a higher value of entropy of any system correlates to a higher symmetry and a higher indistinguishability of both dynamic systems and static structures [2].
This theory [2] is useful for characterizing structural stability and process spontaneity.
[1] The resolution of this paradox has been very controversial. Some recent debates are: (a) Lesk, A. M. On the Gibbs paradox: what does indistinguishability really mean? J. Phys. A: Math. Gen. 1980, 13, L111-L114; (b) van Kampen, N. G. The Gibbs Paradox, In Essays in Theoretical Physics; Parry, W. E., Ed.; Pergamon: Oxford, 1984, 303-312; (c) Kemp, H. R. Gibbs' paradox: Two views on the correction term. J. Chem. Educ. 1986, 63, 735-736; (d) Dieks, D.; van Dijk, V. Another look at the quantum mechanical entropy of mixing. Am. J. Phys. 1988, 56, 430-434; (e) Richardson, I. W. The Gibbs paradox and unidirectional fluxes. Eur. Biophys. J. 1989, 17, 281-286; (f) Lin, S.-K. Gibbs paradox and its resolutions. Ziran Zazhi 1989, 12, 376-379. (g) Wantke, K. -D. A remark on the Gibbs-paradox of the entropy of mixing of ideal gases. Ber. Bunsen-Ges. Phys. Chem. 1991, 94, 537; (h) Jaynes, E. T. The Gibbs Paradox, In Maximum Entropy and Bayesian Methods; Smith, C. R.; Erickson, G. J.; Neudorfer, P. O., Eds.; Kluwer Academic: Dordrecht, 1992, p.1-22; (i) Blumenfeld, L. A.; Grosberg, A. Y. Gibbs paradox and the notion of construction in thermodynamics and statistic physics. Biofizika 1995, 40, 660-667.
[2] (a) Lin, S.-K. Correlation of entropy with similarity and symmetry. J. Chem. Inf. Comp. Sci. 1996, 36, 367-376. (b) Lin, S.-K. Gibbs paradox of entropy of mixing: experimental facts, its rejection and the theoretical consequences. J. Theor. Chem. 1996, 1, 135-150; (c) Lin, S. -K. Molecular diversity assessment: Logarithmic relations of information and species diversity and logarithmic relations of entropy and indistinguishability after rejection of Gibbs paradox of entropy of mixing. Molecules 1996, 1, 57-67. (d) Lin, S.-K. Understanding structural stability and process spontaneity based on the rejection of the Gibbs paradox of entropy of mixing. J. Mol. Struct. Theochem 1997, 398, 145-153. (e) Lin, S.-K. Symmetry breaking problem resolved (American Physical Society Meeting, Kansas City, MO, March 17-21, 1997). Bull. Am. Phys. Soc. 1997, 42, 679. (f) Lin, S.-K. The nature of the chemical process. A new information theory. The 36th IUPAC Congress, Geneva, Switzerland, August 17-22, 1997. Chimia 1997, 51, 515.
[3] "The symmetry group of the cause is a subgroup of the symmetry group of the effect". See: Rosen, J. Symmetry in Science; Springer: New York, 1995; p. 191.
[4] Semantically, the Greek word symmetry means same measure or indistinguishability measure.