Shu-Kun Lin
Molecular Diversity Preservation International (MDPI)
Saengergasse 25,
CH-4054 Basel, Switzerland (email: [email protected])
The relations of the two most important concepts, entropy and symmetry, are mathematically clarified. It has been a tacit assumption that higher symmetry of a system imply less entropy. However, it is proved here that the opposite is true for both dynamic and static systems. Higher value of entropy of any system is correlated to higher symmetry. Entropy (S) of a system of w microstates is expressed as a logarithmic function of symmetry,
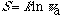
The apparent symmetry number is
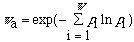
where
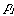is the probability of the ith microstate.
This relation is broadly useful for solving problems of relative structural stability of both dynamic systems and static structures [1-4].
[1] S.-K. Lin, J. Chem. Inf. Comp. Sci. 1996, 36, 367-376.
[2] S.-K. Lin, J. Theor. Chem. 1996, 1, 135-150. This paper is downloadable from http://www.mdpi.org/lin.htm.
[3] (a) S.-K. Lin, Understanding structural stability and process spontaneity based on the rejection of the Gibbs paradox of entropy of mixing. Paper presented at the Fourth World Congress of Theoretically Oriented Chemists, Jerusalem, Israel, July 7-12, 1996.
(b) S.-K. Lin, J. Mol. Struct. Theochem 1997, 398, 145-154.
[4] S.-K. Lin, Symmetry-breaking problem resolved. Paper accepted for presentation at the American Physical Society 1997 March Meeting, Kansas City, MO, March 17-21, 1997. Abstract downloadable from http://www.aps.org/BAPSMAR97/abs/S4580004.html.