Presented at the 36th IUPAC Congress, Geneva, Switzerland, August 17-22, 1997.
(Abstract published in Chimia, 1997, 51, 515.)
The Nature of the Chemical Process. A New Information Theory
Shu-Kun Lin
Molecular Diversity Preservation International (MDPI)
Sängergasse 25,
CH-4054 Basel, Switzerland ([email protected])
Statistical mechanics is the foundation of thermodynamics. Information theory
is regarded as the foundation of statistical mechanics. However, it might be a
surprise that information theory has never been practically used to the
thermodynamic or statistical mechanics problems in chemistry so far. Structural
stability and process spontaneity have been characterized by entropy
(information loss).
According to Gibbs, entropy of mixing decreases discontinuously with the
increase in molecular or quantum state similarity. It also implies that entropy
(S) of a system decreases with the increase in its symmetry, or
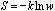 (w: the symmetry number, e.g., the permutation symmetry number N!
of an ideal gas of N particles). It is assumed that these relations of
entropy are applicable to the formation of a solid, liquid, or gaseous mixture
and to the mixing of quantum states involved in all kinds of chemical
processes.
(w: the symmetry number, e.g., the permutation symmetry number N!
of an ideal gas of N particles). It is assumed that these relations of
entropy are applicable to the formation of a solid, liquid, or gaseous mixture
and to the mixing of quantum states involved in all kinds of chemical
processes.
A large number of chemical and physical observations have been presented to
show that the Gibbs statement of mixing is itself wrong [1,2a]. The Gibbs
statement is proved [2a] to be false by considering the entropy additivity
principle, the basic principle of group theory, and the inequality
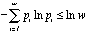 .
Finally,
.
Finally,
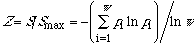 (where
(where
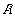 is the probability) defines a similarity index [2b]. Entropy increases
continuously with the property similarity of the w microstates or the
subsystems. Entropy also increases with the symmetry [1]:
is the probability) defines a similarity index [2b]. Entropy increases
continuously with the property similarity of the w microstates or the
subsystems. Entropy also increases with the symmetry [1]:
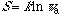 (where
(where
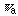 is the apparent symmetry number). The new information theory [1-2] is
applicable to chemical process problems of mixing, self-organization, chemical
bonding and deformation [2a,3].
is the apparent symmetry number). The new information theory [1-2] is
applicable to chemical process problems of mixing, self-organization, chemical
bonding and deformation [2a,3].
References
[1] S.-K. Lin, J. Chem. Inf. Comp. Sci. 1996, 36,
367-376.
[2] (a) S.-K. Lin, J. Theor. Chem. 1996, 1, 135-150. (b)
S.-K. Lin, Molecules 1996, 1, 57-67. These two papers are
downloadable from http://www.mdpi.org/lin.htm.
[3] Lin, S.-K. J. Mol. Struct. Theochem 1997, 398,
145-154.
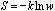 (w: the symmetry number, e.g., the permutation symmetry number N!
of an ideal gas of N particles). It is assumed that these relations of
entropy are applicable to the formation of a solid, liquid, or gaseous mixture
and to the mixing of quantum states involved in all kinds of chemical
processes.
(w: the symmetry number, e.g., the permutation symmetry number N!
of an ideal gas of N particles). It is assumed that these relations of
entropy are applicable to the formation of a solid, liquid, or gaseous mixture
and to the mixing of quantum states involved in all kinds of chemical
processes.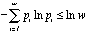 .
Finally,
.
Finally,
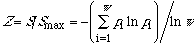 (where
(where
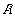 is the probability) defines a similarity index [2b]. Entropy increases
continuously with the property similarity of the w microstates or the
subsystems. Entropy also increases with the symmetry [1]:
is the probability) defines a similarity index [2b]. Entropy increases
continuously with the property similarity of the w microstates or the
subsystems. Entropy also increases with the symmetry [1]:
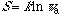 (where
(where
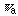 is the apparent symmetry number). The new information theory [1-2] is
applicable to chemical process problems of mixing, self-organization, chemical
bonding and deformation [2a,3].
is the apparent symmetry number). The new information theory [1-2] is
applicable to chemical process problems of mixing, self-organization, chemical
bonding and deformation [2a,3].