Presented at the New Swiss Chemical Society (NSCS) Fall Meeting, Universite de
Lausanne, 15 October 1997.
(Abstract published in Chimia, 1997,
51, 646)
Physical Chemistry, Poster 229
Gibbs Paradox of Entropy of Mixing
Shu-Kun Lin
MDPI Center, Sängergasse 25, CH-4054, Basel ([email protected])
Gibbs paradox says that entropy of mixing decreases discontinuously with
the increase in molecular similarity. It also implies that entropy (S)
of a system decreases with the increase in its symmetry, or
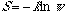 (
(
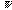 :
the symmetry number, e.g., the permutation symmetry number N! of an
ideal gas of N particles). It is assumed that these relations of entropy
are applicable to the formation of a solid, liquid, or gaseous mixture and to
the mixing of quantum states. A large number of chemical and physical
observations have been presented to show that the Gibbs paradox of mixing is
itself wrong [1]. It is shown here that the Gibbs paradox statement is false.
We disprove it firstly through the entropy additivity principle, Secondly, from
group theory, any system has a symmetry number
:
the symmetry number, e.g., the permutation symmetry number N! of an
ideal gas of N particles). It is assumed that these relations of entropy
are applicable to the formation of a solid, liquid, or gaseous mixture and to
the mixing of quantum states. A large number of chemical and physical
observations have been presented to show that the Gibbs paradox of mixing is
itself wrong [1]. It is shown here that the Gibbs paradox statement is false.
We disprove it firstly through the entropy additivity principle, Secondly, from
group theory, any system has a symmetry number
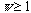 (
(
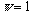 for the identity operation of a strictly asymmetric system). It follows that
the entropy of any system is equal to, or less than, zero, following the Gibbs
paradox statement. This violates the definition of entropy which is
non-negative. Thirdly, Gibbs's statement of entropy and similarity obviously
violates the inequality
for the identity operation of a strictly asymmetric system). It follows that
the entropy of any system is equal to, or less than, zero, following the Gibbs
paradox statement. This violates the definition of entropy which is
non-negative. Thirdly, Gibbs's statement of entropy and similarity obviously
violates the inequality
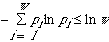 .
In conclusion,
.
In conclusion,
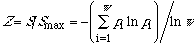 defines a similarity index, and entropy increases continuously with the
property similarity of the w microstates or w subsystems. Entropy
also increases with the symmetry [2]:
defines a similarity index, and entropy increases continuously with the
property similarity of the w microstates or w subsystems. Entropy
also increases with the symmetry [2]:
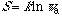 (
(
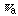 :
the apparent symmetry number). The theoretical consequences in chemistry will
be discussed.
:
the apparent symmetry number). The theoretical consequences in chemistry will
be discussed.
[1] S.-K. Lin, J. Chem. Inf. Comp. Sci. 1996, 36, 367-376.
S.-K. Lin, J. Theor. Chem. 1996, 1, 135-150.
[2] S.-K. Lin, Symmetry breaking problem resolved. Paper presented at
the American Physical Society 1997 March Meeting, Kansas City, MO, March 17-21,
1997.
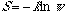 (
(
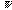 :
the symmetry number, e.g., the permutation symmetry number N! of an
ideal gas of N particles). It is assumed that these relations of entropy
are applicable to the formation of a solid, liquid, or gaseous mixture and to
the mixing of quantum states. A large number of chemical and physical
observations have been presented to show that the Gibbs paradox of mixing is
itself wrong [1]. It is shown here that the Gibbs paradox statement is false.
We disprove it firstly through the entropy additivity principle, Secondly, from
group theory, any system has a symmetry number
:
the symmetry number, e.g., the permutation symmetry number N! of an
ideal gas of N particles). It is assumed that these relations of entropy
are applicable to the formation of a solid, liquid, or gaseous mixture and to
the mixing of quantum states. A large number of chemical and physical
observations have been presented to show that the Gibbs paradox of mixing is
itself wrong [1]. It is shown here that the Gibbs paradox statement is false.
We disprove it firstly through the entropy additivity principle, Secondly, from
group theory, any system has a symmetry number
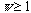 (
(
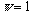 for the identity operation of a strictly asymmetric system). It follows that
the entropy of any system is equal to, or less than, zero, following the Gibbs
paradox statement. This violates the definition of entropy which is
non-negative. Thirdly, Gibbs's statement of entropy and similarity obviously
violates the inequality
for the identity operation of a strictly asymmetric system). It follows that
the entropy of any system is equal to, or less than, zero, following the Gibbs
paradox statement. This violates the definition of entropy which is
non-negative. Thirdly, Gibbs's statement of entropy and similarity obviously
violates the inequality
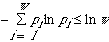 .
In conclusion,
.
In conclusion,
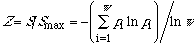 defines a similarity index, and entropy increases continuously with the
property similarity of the w microstates or w subsystems. Entropy
also increases with the symmetry [2]:
defines a similarity index, and entropy increases continuously with the
property similarity of the w microstates or w subsystems. Entropy
also increases with the symmetry [2]:
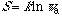 (
(
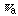 :
the apparent symmetry number). The theoretical consequences in chemistry will
be discussed.
:
the apparent symmetry number). The theoretical consequences in chemistry will
be discussed.