Presented at the New Swiss Chemical Society (NSCS) Fall Meeting, Universite de
Lausanne, 15 October 1997.
(Abstract published in Chimia, 1997,
51, 646)
Physical Chemistry, Poster 231
Negative and Positive Temperatures of Static and Dynamic
Aspects
Shu-Kun Lin
Molecular Diversity Preservation International (MDPI)
Sängergasse 25,
CH-4054 Basel (e-mail: [email protected])
According to definition, total energy
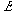 and entropy
and entropy
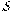 are both positive for any system. However, temperature
are both positive for any system. However, temperature
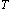 defined as
defined as
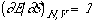 may be either positive or negative [1]. Following this definition and the
general criteria [1] for negative temperature, for any well-defined entropies
of any systems of hierarchical structures, correspondingly temperature(s) can
be defined, at least formally. We found that every system has symmetries of
static and dynamic aspects [2] and the two entropies and their
variations can be defined and in principle calculated according to
may be either positive or negative [1]. Following this definition and the
general criteria [1] for negative temperature, for any well-defined entropies
of any systems of hierarchical structures, correspondingly temperature(s) can
be defined, at least formally. We found that every system has symmetries of
static and dynamic aspects [2] and the two entropies and their
variations can be defined and in principle calculated according to
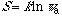 ,
where
,
where
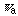 is the apparent symmetry number or the order of the group [2].
is the apparent symmetry number or the order of the group [2].
Therefore, for a conventional thermodynamic system, because information
registration involves reduced static symmetry (
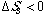 )
[2] and the energy increase (
)
[2] and the energy increase (
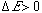 )
[3], a negative temperature
)
[3], a negative temperature
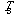 (s for static) can be formally defined, while the dynamic motion of such
system has a conventionally understood positive temperature
(s for static) can be formally defined, while the dynamic motion of such
system has a conventionally understood positive temperature
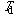 (d for dynamic).
(d for dynamic).
Similarly, however, for a system of electronic motion in a single atom or a
molecule, the
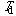 of the local electronic dynamic motion is found to be negative with the
most negative value at the electronic ground state, while its local
of the local electronic dynamic motion is found to be negative with the
most negative value at the electronic ground state, while its local
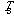 of the static aspect of the electronic structure, such as spin parallel
orientation at excited states, is positive.
of the static aspect of the electronic structure, such as spin parallel
orientation at excited states, is positive.
It is convenient to use these temperatures to characterize symmetry breaking
phenomena at any one of many hierarchical structures in nature.
[1] a) N.F. Ramsey, Phys. Rev. 1956, 103, 20-28. b) C.
Kittel, H. Kroemer, Thermal Physics, Freeman, San Francisco, 1980.
[2] S.-K. Lin, J. Chem. Inf. Comp. Sci. 1996, 36, 367-376.
S.-K. Lin, J. Theor. Chem. 1996, 1, 135-150. S.-K. Lin,
Theochem 1997, in press.
[3] W.G. Teich, G. Mahler, in: Complexity, Entropy and the Physics of
Information, W.H. Zurek (Ed.), Addison-Wesley, Redwood City, California,
1990, p.289.
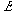 and entropy
and entropy
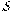 are both positive for any system. However, temperature
are both positive for any system. However, temperature
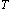 defined as
defined as
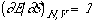 may be either positive or negative [1]. Following this definition and the
general criteria [1] for negative temperature, for any well-defined entropies
of any systems of hierarchical structures, correspondingly temperature(s) can
be defined, at least formally. We found that every system has symmetries of
static and dynamic aspects [2] and the two entropies and their
variations can be defined and in principle calculated according to
may be either positive or negative [1]. Following this definition and the
general criteria [1] for negative temperature, for any well-defined entropies
of any systems of hierarchical structures, correspondingly temperature(s) can
be defined, at least formally. We found that every system has symmetries of
static and dynamic aspects [2] and the two entropies and their
variations can be defined and in principle calculated according to
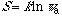 ,
where
,
where
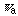 is the apparent symmetry number or the order of the group [2].
is the apparent symmetry number or the order of the group [2].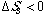 )
[2] and the energy increase (
)
[2] and the energy increase (
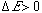 )
[3], a negative temperature
)
[3], a negative temperature
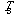 (s for static) can be formally defined, while the dynamic motion of such
system has a conventionally understood positive temperature
(s for static) can be formally defined, while the dynamic motion of such
system has a conventionally understood positive temperature
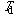 (d for dynamic).
(d for dynamic).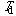 of the local electronic dynamic motion is found to be negative with the
most negative value at the electronic ground state, while its local
of the local electronic dynamic motion is found to be negative with the
most negative value at the electronic ground state, while its local
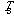 of the static aspect of the electronic structure, such as spin parallel
orientation at excited states, is positive.
of the static aspect of the electronic structure, such as spin parallel
orientation at excited states, is positive.